Cette page est une synthèse faite à partir d'informations contenues dans le site de l'Institut National Géographique (I.G.N.). Elle n'appartient donc pas au S.G.C.A.F.
Je vous conseille vivement d'aller visiter le site de l'I.G.N. il est très bien fait.
SOMMAIRE :
|
|
|
|
Notion de coordonnéesType de coordonnéesCoordonnées géographiquesCoordonnées planesTransformation de coordonnéesUtilisation du G.P.S.Et en spéléo...
|
Pour se localiser sur la terre, il est nécessaire d'utiliser un système géodésique duquel découlent les coordonnées géographiques figurant sur les cartes. Celles-ci peuvent être exprimées soit sous la forme de longitude et latitude (coordonnées dites géographiques), soit en représentation cartographique plane (coordonnées dites en projection).
Sur les cartes des série bleue, TOP 25®, série orange, deux systèmes géodésiques sont figurés sous forme de coordonnées dans la marge :
- Le système européen ED50, en degrés sexagésimaux et en coordonnées planes UTM.
- Le système français NTF, en grades et en coordonnées planes Lambert.
Sur les cartes de la série verte seul figure le système NTF en grades.
Coordonnées géographiques
Exprimées en grades ou en degrés sexagésimaux, les coordonnées géographiques donnent la latitude et la longitude d'un lieu par rapport à un méridien origine :
- système ED50 : méridien de Greenwich dit méridien international
- système NTF : méridien de Paris
Projection et coordonnées planes
Pour les besoins cartographiques, on doit représenter sur une surface plane l'ellipsoïde, image de la terre, ce qui nécessite l'utilisation d'une projection. Les coordonnées planes ainsi obtenues rendent plus faciles les calculs.
Les déformations engendrées par la projection n'ont que très peu d'incidence sur les calculs pour les cartes topographiques à grande échelle. Les projections associées aux systèmes géodésiques utilisés en France sont les suivantes :
- système ED50 : projection cylindrique UTM (Universal Transverse Mercator)
- système NTF : projection conique conforme Lambert
La France métropolitaine est sur 3 fuseaux UTM : UTM Nord fuseaux 30, 31 et 32.
![[Les fuseaux UTM]](/dessins/utm3.gif)
La France métropolitaine est découpée en 4 zones : Lambert I, II, III, IV (Corse). Pour des besoins de représentation globale de la France une projection Lambert II étendu a été créée.
![[Les zones Lambert]](/dessins/lambert3.gif)
Coordonnées figurant sur les cartes topographiques 1/25000
Les deux échelles figurant dans le cadre portent des chiffraisons kilométriques :
- vers l'intérieur :
- en noir, les amorces du quadrillage kilométrique Lambert "zone", c'est-à-dire Lambert I, II, III ou IV. La valeur des Y des coordonnées en "Lambert zone" est toujours précédée du numéro de la zone Lambert (exemple : 3196 = 196 000 m Lambert III).
- en bleu, les amorces du quadrillage kilométrique Lambert II étendu. Le quadrillage Lambert II étendu n'est pas tracé sur la carte mais, en plus des amorces dans la marge, des croisillons à l'intérieur de la carte tous les kilomètres permettent de le reconstituer.
- en grades, les latitudes et longitudes rapportées au système français NTF
- vers l'extérieur :
- en noir, les amorces du quadrillage UTM du fuseau correspondant à la zone; en limite de deux fuseaux, les amorces coexistent en bleu et noir, les valeurs les plus faibles correspondant au fuseau de numéro supérieur.
- en degrés, les latitudes et longitudes rapportées au système ED50
Les coordonnées peuvent être exprimées :
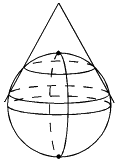
![[Coordonnées géographiques]](/dessins/globe3.gif)
- sous la forme de coordonnées cartésiennes géocentriques (X,Y,Z) relatives aux 3 axes d'un repère ayant son origine au centre des masses de la Terre. Ces coordonnées peuvent être utilisées, par exemple, comme intermédiaire lors de calculs de changements de systèmes géodésiques de références.
- sous la forme de coordonnées géographiques
- La lettre grecque
(lambda) désignant la longitude.
- La lettre grecque
(phi) la latitude.
- La lettre h correspond à la hauteur ellipsoïdale (à ne pas confondre avec l'altitude). Elle est définie dans un système de référence géodésique et peut différer de l'altitude de plusieurs dizaines de mètres.
- en représentation plane (coordonnées dites en "projection")
Contrairement à l'usage, il est préférable d'utiliser la convention E, N (Est, Nord) pour désigner des coordonnées en projection pour éviter toute confusion avec les coordonnées cartésiennes (X, Y, Z).
|
Type de coordonnées |
X,Y,Z |
|
E,N |
|---|---|---|---|
|
Unité angulaire |
|
|
|
|
Unité linéaire |
|
|
|
|
Projection |
|
|
|
|
Méridien origine |
|
|
|
|
Ellipsoïde |
|
|
|
|
Système géodésique |
|
|
|
Notation des unités angulaires pour les latitudes et longitudes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Approches numériques :
|
1° |
= 60´ |
= 3 600" |
|
180° |
= 200 gr |
= 3.141592654 rd |
|
48.61° |
= 48° 36.6´ |
= 48° 36´ 36" |
|
48.60° |
= 54 gr |
|
Un degré de longitude équivaut à environ 111 km sur l'équateur mais ne vaut plus que 74 km à une latitude de 48 degrés et devient 0 km au pôle Nord
En considérant une terre sphérique de rayon 6360 km :
1° de longitude = cosinus(latitude) * 111 km
1° de latitude = 111 km.
Méridien origine
Les longitudes sont le plus souvent comptées positivement vers l'est, par rapport à un méridien origine. Ce méridien origine peut être celui de Greenwich (méridien international), ou encore propre à la géodésie d'un pays (méridien de Paris pour la France). Chaque méridien origine est défini numériquement par sa longitude par rapport au méridien international.
Le méridien de Paris est à 2° 20´ 14.025" à l'est de celui de Greenwich.
L'ellipsoïde de révolution ("sphère aplatie aux pôles") est un modèle mathématique utilisé pour le calcul et que l'on définit pour qu'il soit le plus près possible du géoïde. Il existe de nombreux modèles d'ellipsoïdes. A chaque référentiel géodésique est associé un ellipsoïde sur lequel on a fixé un méridien comme origine des longitudes et qui est parfaitement défini par le demi - grand axe a et une des différentes valeurs :
|
demi grand - axe |
|
|
demi petit - axe |
|
|
inverse de l'aplatissement |
|
|
première excentricité |
|
|
carré de l'excentricité |
|
|
deuxième excentricité |
|
Modèles d'ellipsoïde en usage en France
|
Système |
Ellipsoïde |
a |
b |
1/f |
e |
|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cette valeur est définie dans un système géodésique et peut différer de l'altitude de plusieurs dizaines de mètres. Elle correspond à une distance entre le point considéré et le pied de la normale à l'ellipsoïde. Tous les systèmes de positionnement par satellites fournissent une hauteur ellipsoïdale et non une altitude.
Il existe des modèles de géoïde (formules de conversion d' hauteur sur ellipsoïde vers une altitude (type nivellement) permettant de passer de valeurs d'altitudes à des hauteurs ellipsoïdales avec une précision décimétrique. Il est possible très localement d'assimiler des différences de hauteurs ellipsoïdales à des différences d'altitudes. En faisant cela on néglige la "pente du géoïde" (correspondant à l'écart entre la verticale et la normale à l'ellipsoïde), qui est plus importante en région montagneuse.
On utilise une représentation plane de la terre ou projection afin
- de représenter sur une surface plane une partie d'un modèle ellipsoïdal de la surface de la terre.
- d'obtenir des valeurs métriques plus exploitables que l'unité angulaire.
- de rendre plus facile une évaluation des distances.
Mais une projection ne peut jamais se faire sans qu'il y ait de déformations. Pour s'en convaincre, il suffit d'essayer d'aplatir la peau d'une orange !
Néanmoins, par calcul, il est possible de définir le type et les paramètres d'une projection dans le but de minimiser certaines déformations. On choisit alors :
- soit de conserver les surfaces (projections équivalentes)
- soit de conserver localement les angles (projections conformes)
- soit d'opter pour une représentation ne conservant ni les angles ni les surfaces (projections dites "aphylactiques").
Une projection dite "équidistante" conserve les distances à partir d'un point donné. Dans tous les cas, aucune projection ne peut conserver toutes les distances. On introduit alors les notions de module linéaire et d'altération linéaire. Aujourd'hui, la plupart des projections utilisées en géodésie et topographie sont conformes. La cartographie à petite échelle utilise souvent des projections équivalentes.
Dans la plupart des projections, le Nord de la projection n'indique pas la direction du pôle Nord géographique. On introduit alors la notion de convergence des méridiens définie comme suit : la convergence des méridiens en un point est le gisement de l'image (dans la projection) du méridien qui passe par ce point.
Sur une carte donnée, les valeurs de convergence des méridiens et de module linéaire (donc d'altération linéaire) sont variables selon la position du point.
Aux notions de Nord géographique et de "Nord de la projection", on peut ajouter celle de Nord magnétique. L'angle entre le Nord magnétique et le Nord géographique s'appelle déclinaison magnétique.
Principaux groupes de projections
Projection cylindrique : la surface de projection est un cylindre tangent ou sécant au modèle de la Terre. (Exemple : UTM, Gauss,...)
 représentation cylindrique directe |
 représentation cylindrique oblique |
 représentation cylindrique transverse |
Projection conique : la surface de projection est un cône tangent ou sécant. (Exemple : Lambert, Lambert93,...)
 représentation conique directe tangente |
 représentation conique directe sécante |
Projection azimutale : le plan lui même est tangent au modèle de la terre. (Exemple : Stéréographie polaire (carte du ciel, cartes des régions polaires,...)
Les intersections entre le plan de projection et l'ellipsoïde forment des lignes appelées automécoïques.
Lambert : Projection associée au système géodésique NTF
La projection règlementaire en France est une conique conforme de Lambert. Dans le but de minimiser les déformations (altérations linéaires), la France a été découpée en 4 zones. Une projection appelée "Lambert II étendu" couvre la France entière pour des besoins d'amplitude nationale.
Les valeurs suivantes permettent le calcul des coordonnées en projection Lambert de l'ellipsoïde de Clarke 1880 IGN.
|
Zone lambert |
I |
II |
III |
IV |
II étendu |
|---|---|---|---|---|---|
|
Zone application |
|
|
|
|
|
|
Latitude origine |
|
|
|
|
|
|
Longitude origine |
|
|
|
|
|
|
Parallèles |
50°23´45.282" |
47°41´45.652" |
44°59´45.938" |
42°46´03.588" |
47°41´45.652" |
|
X0 : False Easting |
|
|
|
|
|
|
Y0 : False Northing |
|
|
|
|
|
Remarques :
Les projections Lambert de la France sont en fait, par définition, des projections tangentes avec facteur d'échelle, les valeurs précédemment fournies sont celles des projections sécantes correspondantes car ce sont elles qui sont requises pour l'utilisation de certains récepteurs GPS.
Sur les cartes topographiques au 1 : 25 000 les valeurs des Y (ou N) sont exprimées en kilomètres et précédées du numéro de la zone (sauf pour le Lambert II étendu).Exemple : N = 196 000 m devient 3 196 pour la carte du mont Ventoux (Lambert III)
UTM : Projection associée au système géodésique Europe Datum 50
La projection cylindrique UTM (Universal Transverse Mercator) couvre le monde entier et est constituée de 60 fuseaux de 6 degrés d'amplitude en longitude.
La France est sur 3 fuseaux :
- UTM Nord fuseau 30 : entre 6 degrés ouest et 0 degré Greenwich
- UTM Nord fuseau 31 : entre 0 degré et 6 degrés est Greenwich
- UTM Nord fuseau 32 : entre 6 degrés est et 12 degrés est Greenwich
|
Référentiel géodésique associé |
ED50 |
|
Ellipsoïde associé |
International (Hayford 1909) |
|
X0 (False Easting) |
500 000 m |
|
Y0 (False Northing) |
0 m |
|
Longitude origine |
-3°, 3°, 9° Est
Greenwich |
|
Facteur d'échelle |
0.9996 |
Remarque : On emploie également la projection UTM associée à d'autres référentiels géodésiques (comme le WGS84), donc avec d'autres ellipsoïdes (IAG GRS 1980 pour le WGS84).
Lambert-93 : Projection associée au système géodésique RGF93
Une projection conique conforme sécante de Lambert appelée "Lambert-93" a été retenue en septembre 1996 pour une utilisation cartographique du nouveau système géodésique français RGF93. Elle n'apparaît pas encore reportée sur les cartes topographiques.
|
Référentiel géodésique |
RGF93 |
|
Ellipsoïde associé |
IAG GRS80 |
|
X0 (False Easting) |
700 000 m |
|
Y0 (False Northing) |
6 600 000 m |
|
Latitude origine |
46°30´nbsp;N |
|
Longitude origine |
3° Est Greenwich |
|
Parallèles automécoïques |
44° N et 49° N |
La navigation a beaucoup évolué avec l'usage du GPS qui fournit une position absolue dans un système géodésique donné. La notion de "changement de système" prend alors toute son importance pour ne pas obtenir des résultats grossièrement erronés, le décalage pouvant atteindre plusieurs centaines de mètres. Prenons par exemple un point situé dans l'est de la France, les coordonnées suivantes expriment la position du même détail (à trois mètres près) :
|
Longitude ou E |
Latitude ou N |
Système de coordonnées |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Processus de changement de système
Un changement de système géodésique s'effectue le plus souvent au niveau des coordonnées cartésiennes géocentriques (XYZ). Si vous disposez de coordonnées géographiques
vous devrez donc les transformer en cartésiennes géocentriques, et si vous travaillez en projection, il vous faudra passer tout d'abord en géographiques, puis en cartésiennes géocentriques.
Certains récepteurs GPS proposent une liste de systèmes géodésiques voire, parfois, d'entrer soi-même des valeurs de translations. Pour certaines applications plus fines, on devra associer aux translations précédentes des rotations (suivant chaque axe) et un facteur d'échelle.
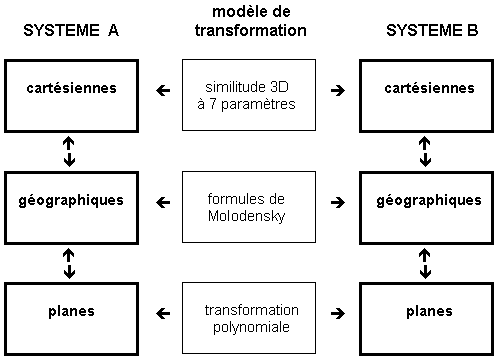
Le plus utilisé est la similitude 3D car elle présente l'avantage de pouvoir être utilisée "dans les 2 sens" (Les mêmes 7 paramètres servent à transformer des coordonnées exprimées dans le système A vers le système B mais également du système B vers le système A).
Les formules de Molodensky sont des développements limités dont l'ordre influe évidemment sur la précision finale. Le passage inverse nécessite l'application de formules différentes.
La transformation polynomiale ne s'applique que sur des zones restreintes (pour conserver une précision comparable à celle obtenue par l'emploi d'une similitude).
Utilisation pratique des paramètres de passage NTF --> WGS84
Le système NTF n'étant pas toujours implémenté dans les récepteurs GPS, il conviendra d'utiliser les paramètres suivants, pour la similitude, recommandés à l'IGN : (dits " standards" pour la France)
NTF vers WGS84 : TX = -168 m TY = -60 m TZ = +320 m.
pour une précision sur les coordonnées de quelques mètres. Une précision centimétrique ne peut être obtenue que par l'utilisation d'une grille de paramètres dans laquelle les valeurs de translations sont interpolées. Cela permet de prendre en compte les déformations de la NTF liées aux techniques de triangulation mises en oeuvres.
|
|
Le système GPS donne des coordonnées dans le système WGS84 dont la représentation ne figure pas systématiquement sur les cartes topographiques. Depuis le 1er mars 1999, les cartes de randonnées (série bleue et TOP 25 uniquement) nouvellement éditées ou rééditées sont en effet pourvues d'un quadrillage kilomètrique UTM / WGS84 permettant d'établir un lien réciproque entre la carte et le GPS. |
Lors de l'utilisation d'un GPS avec une carte IGN, vous pouvez avoir besoin de connaître les coordonnées GPS d'un point identifié sur la carte ou, inversement, d'identifier sur la carte un point dont vous connaissez les coordonnées GPS.
Les lignes suivantes vous permettent d'établir la correspondance entre les différents systèmes utilisés sur les cartes IGN et le GPS.
Attention, les formules indiquées ne donnent pas une précision suffisante pour des applications techniques, il faut alors vous reporter aux pages Géodésie et Nivellement.
C'est le récepteur GPS qui permet ou non le changement de système de référence pour vous adapter aux cartes en usage en France.
Pour déterminer les coordonnées GPS d'un point figurant sur une carte à l'échelle du 1 : 100 000 (série verte) il est nécessaire d'appliquer la formule de conversion des coordonnées donnée ci-dessous :
Conversion NTF --> WGS84, précision de 100 m.
Exemple de la carte à l'échelle du 1 : 100 000.
![[Chatel - Extrait 45 Ed. 97]](/dessins/Chatel45.gif)
Pour un calcul avec cette précision, il est possible de confondre les systèmes NTF et WGS84, il suffit alors d'appliquer des formules simples décomposées comme suit :
- Lire les coordonnées en grades à l'aide des amorces figurant sur la carte,
attention au signe des coordonnées suivant la position par rapport au méridien de Paris.- Transformer les grades en degrés décimaux (400 grades = 360° ; 1 grade = 0,9°),
- transformer les degrés décimaux en degrés sexagésimaux (degrés, minutes, secondes) :
Par exemple : 3,5721° décimaux
= 3 degrés + 0,5721 X 60 minutes
= 3 degrés + 34,326 minutes
= 3 degrés + 34 minutes + 0,326 X 60 secondes
= 3 degrés 34 minutes 19,56 secondes
= 3° 34' 19,56"- On ajoute toujours 2° 20' 14,025" à la longitude obtenue (décalage entre les méridiens de Greenwich et de Paris).
3° 34' 19,56" + 2° 20' 14,025" = 5° 54' 33,585"Exemples :
|
Conversion NTF --> WGS84 | ||
|---|---|---|
|
Lieux |
Longitude NTF |
Latitude NTF |
|
AIX-LES-BAINS |
3,969 grades |
50,771 grades |
|
REDON |
-4,907 grades |
52,948 grades |
|
Transformation de grades en degrés décimaux | ||
|
AIX-LES-BAINS |
3,5721° décimaux |
45,6939° décimaux |
|
REDON |
-4,4163° décimaux |
47,6532° décimaux |
|
Transformation de degrés décimaux en degrés sexagésimaux | ||
|
AIX-LES-BAINS |
3° 34' 19,560" |
45° 41' 38,040" |
|
REDON |
-4° 24' 58,680" |
47° 39' 11,520" |
|
Changement de méridien --> coordonnées "WGS84" | ||
|
AIX-LES-BAINS |
3° 34'
19,560" |
45° 41' 38,040" |
|
REDON |
-4° 24'
58,680" |
47° 39' 11,520" |
Nota : Si l'on dispose d'une calculette munie des conversions HR et HMS cela est un peu plus facile ;)
La même technique peut être utilisée sur les cartes série bleue, TOP 25® et série orange, attention toutefois à la précision des résultats qui est inférieure à la précision de ces cartes - tout en restant suffisante pour se repérer à l'aide d'un GPS.
Si vous souhaitez obtenir des résultats plus précis, il faut utiliser des formules de transformation plus complètes
Suivant la complexité de votre GPS, les coordonnées lues pourront être de quatre types :
|
|
Ces quatre systèmes de coordonnées figurent sur les cartes à l'échelle du 1 : 25 000 et 1 : 50 000 |
Dans les différents cas ci-dessous, les coordonnées sont lues sur le GPS et reportées sur la carte par interpolation à l'aide des informations contenues dans les marges.
|
GPS |
Entrer dans le menu USER de votre GPS et sélectionner le système ED50. |
|---|---|
|
CARTE |
Les latitudes et longitudes correspondantes figurent en italique, dans la marge des cartes, à l'extérieur, en degrés sexagésimaux (ex : 47° 20' 27"). |
|
GPS |
Entrer dans le menu USER de votre GPS et sélectionner le système ED50 ; choisir (si disponible) l'option UTM en précisant le fuseau : 30, 31 ou 32. |
|---|---|
|
CARTE |
Les coordonnées kilométriques figurent en noir en italique, à l'extérieur, seules les amorces du quadrillage permettent de lire des coordonnées sur la carte (ex: 5247, 677). |
|
GPS |
Entrer les paramètres
correspondant au système NTF (de NTF vers WGS84)
: |
|---|---|
|
CARTE |
Les coordonnées en grades figurent à l'intérieur du cadre en noir, les lignes dans la carte représentent les méridiens et les parallèles (ex: 52,60 gr). |
|
GPS |
Même opération que pour les grades. |
|---|---|
|
CARTE |
Les coordonnées kilométriques sont aussi à l'intérieur dans la projection Lambert zone en noir ou bleu (ex: 2265, 373). |
|
|
Une dernière astuce, si vous avez un trou de mémoire, reportez vous à la légende des cartes qui vous rappelle les différents systèmes de coordonnées, leur position dans la marge et la référence du fuseau UTM de la carte concernée (système géodésique unifié = ED50 ; système géodésique français = NTF). |
Le systéme de coordonnées utilisé est le LAMBERT ZONE II ETENDU (chiffres de couleur bleue de l'échelle intérieure sur les cartes I.G.N. au 1/25000).